Limita vektorové funkce
Příklad. Uvažujme funkci \(f:\mathbb{R}\to \mathbb{R}^2\) definovanou předpisem \(f(t)=(\cos(t),\sin(t)).\) Ukažme, že \[ \lim_{t\to 0}f(t)=f(0)=(1,0). \] Zvolme tedy libovolné \(\varepsilon>0\) a hledejme takové \(\delta>0\) aby platilo: \[ |t|<\delta\implies [(\cos t-1)^2+(\sin t)^2]^{1/2}<\varepsilon. \] Položme \(u=\cos t-1\) a \(v=\sin t.\) Pak máme: \[ \begin{eqnarray} [(\cos t-1)^2+(\sin t)^2]^{1/2}&=&(u^2+v^2)^{1/2}\\ &\le& (|u|^2+2|u||v|+|v|^2)^{1/2}\\ &=&|u|+|v|=|\cos t-1|+|\sin t|, \end{eqnarray} \] Nyní vzhledem ke spojitosti funkcí \(\sin t\) a \(\cos t\) lze nalézt \(\delta>0\) tak, že \[|t|<\delta\implies |\cos t-1|<\frac{\varepsilon}{2} \text{ a } |\sin t|<\frac{\varepsilon}{2}.\] Poslední implikace již stačí k důkazu vzhledem k předešlé nerovnosti.
Bez důkazu uveďme větu, která zobecňuje předchozí postup.
Věta. Předpokládejme, že máme dáno zobrazení \(f=(f_1,\ldots,f_m):A\to\mathbb{R}^m,\) \(A\subset\mathbb{R}^n\), \(a\) je hromadným bodem množiny \(A\), \(b=(b_1,\ldots,b_m)\in\mathbb{R}^m.\) Potom platí \[\lim_{x\to a}f(x)=b,\] právě když \[\lim_{x\to a}f_i(x)=b_i,\ \ \ i=1,\ldots,m.\]
Spojitost zobrazení
Definice. Mějme dán metrický prostor \((M,d),\) \(A\subset M,\) \(a\in A.\) Není-li bod \(a\) hromadným bodem množiny \(A,\) nazýváme jej izolovaným bodem množiny \(A.\)
Definice. Mějme dány dva metrické prostory \((M,d)\) a \((N,e),\) \(A\subset M,\) \(a\in A,\) \(f:A\to N.\) Řekneme, že zobrazení \(f\) je spojité v bodě \(a\) je-li bod \(a\) izolovaným bodem množiny \(A\) a nebo pokud je bod \(a\) hromadným bodem množiny \(A\) a platí \[\lim_{x\to a}f(x)=f(a).\]
Cvičení. Ukažte, že zobrazení \(f:M\to N\) metrického prostoru \(M\) do metrického prostoru \(N\) je spojité, právě když je spojité v každém bodě prostoru \(M.\)
Cvičení. Uvažujme zobrazení \(\pi_i:\mathbb{R}^n\to\mathbb{R},\) \(i\in\{1,\ldots,n\}\) definované předpisem \(\pi_i(x_1,\ldots,x_n)=x_i.\) Dokažte spojitost tohoto zobrazení.
Příklad. Uvažujme dvě funkce \(s\) a \(p\) definované na prostoru \(\mathbb{R}^2\) předpisem \(s(x,y)=x+y\) a \(p(x,y)=xy\) pro každé \((x,y)\in\mathbb{R}^2.\) Potom jsou obě funkce na \(\mathbb{R}^2\) spojitými funkcemi.
Připomeňme si pojem složeného zobrazení. Uvažujme tři metrické prostory \((X,d_1),\)\((Y,d_2)\)a \((Z,d_3).\) Dále mějme dány množiny \(D,D_1\subset X\), \(D_2\subset Y\) a zobrazení \(f:D_1\to Y\), \(g:D_2\to Z\) a předpokládejme, že \[ D=\{x\in X\mid x\in D_1\textrm{ a } f(x)\in D_2\}. \] Pak definujeme tzv. složené zobrazení \(g\circ f:D\to Z\)předpisem: \((g\circ f)(x)=g(f(x)),\)pro \(x\in D.\)
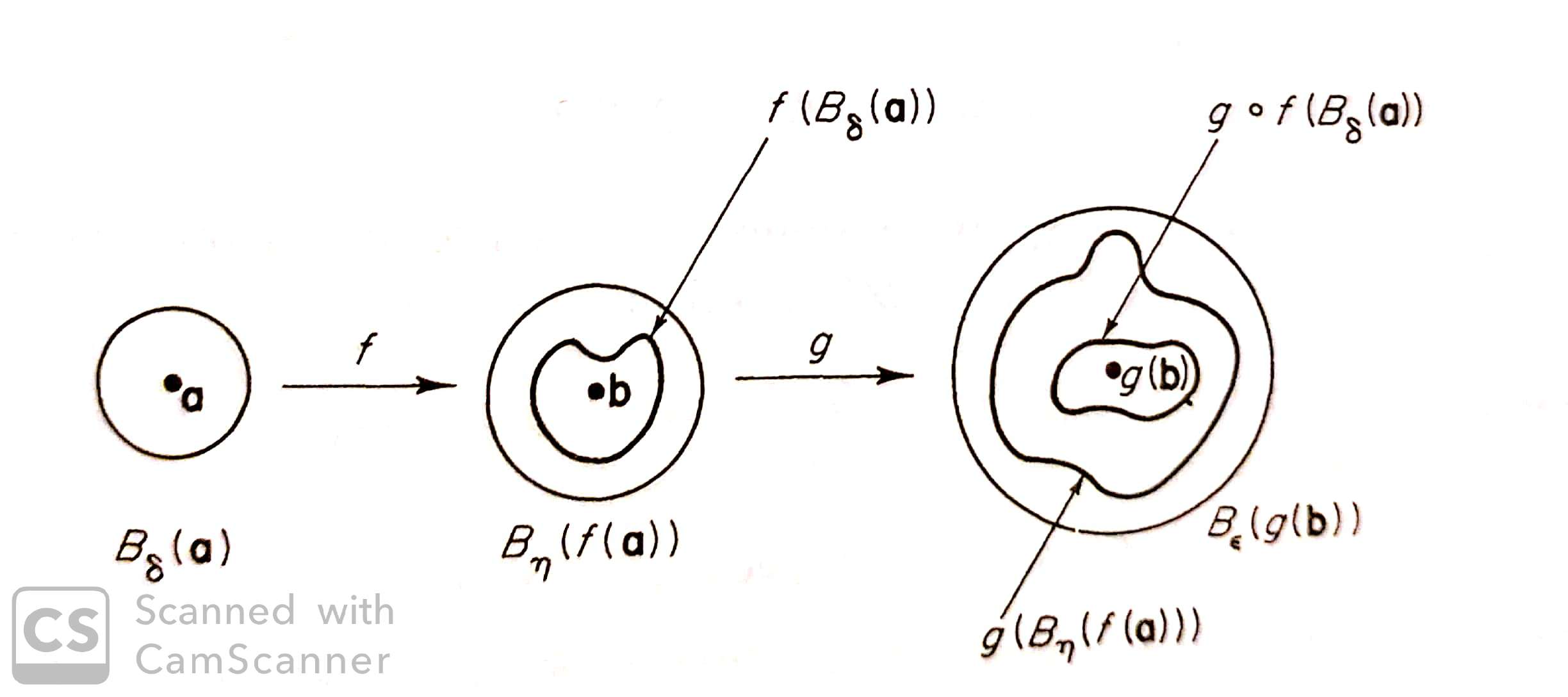
Věta. Nechť jsou dány zobrazení \(f:D_1\to \mathbb{R}^m,\)\(g:D_2\to\mathbb{R}^k,\)kde \(D_1\subset \mathbb{R}^n,\)\(D_2\subset \mathbb{R}^m.\)Předpokládejme, že \[ \lim_{x\to a}f(x)=b, \] a \[ g \textrm{ je spojité zobrazení v bodě }b. \] Potom platí \[ \lim_{x\to a}(g\circ f)(x)=g(b). \]
Věta. Je-li \(f\) funkce spojitá v bodě \(a\), \(g\) funkce spojitá v bodě \(f(a)\), potom je složená funkce \(g\circ f\) spojitá v bodě \(a.\)
Věta. Nechť \(f\)a \(g\) jsou reálné funkce definované na prostoru \(\mathbb{R}^n.\) Potom platí \[ \lim_{x\to a}(f(x)+g(x))=\lim_{x\to a}f(x)+\lim_{x\to a}g(x) \] a \[ \lim_{x\to a}f(x)g(x)=(\lim_{x\to a}f(x))(\lim_{x\to a}g(x)), \] pokud limity na pravých stranách existují.
Cvičení Dokažte předchozí větu.
Příklad.
Uvažujme funkci \(f:\mathbb{R}^3\to\mathbb{R}\)definovanou předpisem \(f(x,y,z)=\sin(x+\cos yz).\)Potom je tato funkce spojitou funkcí.
Jelikož je možné vyjádřit funkci \(f\)jako složenou funkci: \[f=\sin\circ(s\circ(\pi_1,\cos\circ p\circ(\pi_2,\pi_3))),\]je funkce \(f\)skutečně spojitou funkcí.